Financial Cryptography

GP1 - Growth and Fraud - Meet at the Grigg Point

Imagine if you will a successful FC system on the net. That means a system with value, practically, but for moment, keep close in your mind your favourite payments system. Success means solid growth, beyond some point of survival, into the area where growth is assured. It looks like this:

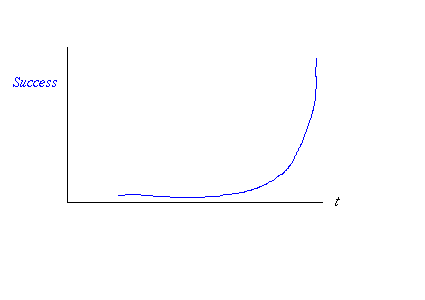
fig 1. Exponential Growth

That's an exponential curve, badly drawn by hand. It's exponential because that's what growth means; all growth and shrinkage is exponential. Let's draw that as a logarithmic curve, so we see a straight line:

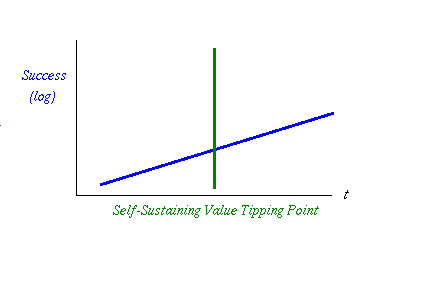
fig 2. Growth Crosses the Value Tipping Point

I've observed in many businesses of monetary nature that there is a special tipping point. This is where the system transitions from being a working demo that is driven forwards by the keenness of its first 100 or so users, to being a system where the value in the system is inherent and cohesive. In and of itself, the value in the system is of such value that it changes the dynamics of the system.

That's why I labelled it the Self-Sustaining Value Growth Tipping Point, or GP for short. Before this point, the system will simply stop if we the founders or we the users stop pushing. After this point, there is a sustained machine that will keep rolling on, creating more and more activity. In short, it's unstoppable, at least as compared to beforehand.

The shortened term indicates who to blame when you reach that point, because there is something else that is going to happen here: fraud! When the system passes GP, and the value is now inherently stealable for its value, then someone will come along and try to steal it.

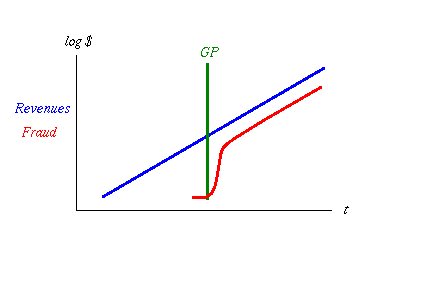
fig 3. Fraud Kicks Off then Levels Off

And that theft will probably work, if history is any judge. You'll get a rash of frauds breaking out, either insider or outsider fraud, and all will appear to be chaos. Actually, it's not chaos, it's just competition for different fraud models, and soon it will settle down to a set of best practices in fraud. At this point, when all the mistakes have been made and the surviving crooks know what they are about, fraud will rise rapidly, then asymptotically approach its long run standard level. Ask any credit card company.

Remember that the graph above has a logarithmic vertical axis, so vertical distances of small amounts mean big distances in absolute amounts. The long run gap between those lines - red to blue - is about two if the vertical was log 10. Assuming that, 10² gives us 100 which means fraud is 1% of total at any time. 1% is a good benchmark, a great number to use if you have no other number, even if the preceeding mathematics are rather ropey. Some systems deliver less, some deliver more, it all depends, but we're in the right area for a log chart.

Now that we have the model in place, what can we do with GP? Quite a lot, it seems, but that waits for the next exciting installment of Growth and the Big GP!

---

This is Part 1 of Growth and Fraud:

• GP1 - Meet at the Grigg Point
• GP2 - Instructing Security at GP
• GP3 - How to Book a Table
• GP4: Case Studies:
  • #1: Mutual Funds
  • #2: e-gold
  • #3: Phishing

Posted by iang at December 11, 2005 03:21 PM | TrackBack